五角十二面體
 | ||||
| 類別 | 凸多面體 | |||
|---|---|---|---|---|
| 對偶多面體 | 扭棱四面體 | |||
| 數學表示法 | ||||
| 考克斯特符號 | ||||
| 性質 | ||||
| 面 | 12 | |||
| 邊 | 30 | |||
| 頂點 | 20 | |||
| 歐拉特徵數 | F=12, E=30, V=20 (χ=2) | |||
| 組成與佈局 | ||||
| 面的種類 | 12個不等邊五邊形 | |||
| 對稱性 | ||||
| 對稱群 | Th, [4,3+], (3*2), order 24 | |||
| 旋轉對稱群 | T, [3,3]+, (332), order 12 | |||
| 特性 | ||||
| 凸, 等面 | ||||
| 圖像 | ||||
| ||||
在幾何學中,五角十二面體[1](Pentagonal dodecahedron或Pyritohedron)是一種由12個不等邊五邊形組成的十二面體,具有四面體群對稱性。其與正十二面體類似,皆是由12個全等的五邊形組成,且每個頂點都是3個五邊形的公共頂點[2],但由於其面不是正多邊形,其頂點的排佈未能達到五摺對稱性,因此不屬於正多面體。部分的化學物質或礦石[3]其晶體形狀是這種形狀,例如黃鐵礦和部分的天然氣水合物[4]。其英文名稱Pyritohedron是來自黃鐵礦的英文pyrite以及多面體的字尾-hedron命名的。[5]
性質
[編輯]五角十二面體是一種等面十二面體,共由12個面、30條邊和20個頂點所組成,其結構在拓樸上與正十二面體相同,但由於構成面不是正多邊形,因此不是正多面體[6]。其30條邊可以分成2組等長的邊,其中一組為24條等長的短邊,另一組為6條等長的長邊。
頂點座標
[編輯]五角十二面體可以透過將立方體6個面的每個面分割成2個矩形,並且相鄰面方向互相垂直的結構變形而來[7],因此五角十二面體中會有8個頂點跟立方體相同,這些頂點的座標為:
- (±1, ±1, ±1)
在將立方體每個面分割成2個矩形時產生的另外12個頂點可以表示為:[8]
- (0, ±(1 + h), ±(1 − h2))
- (±(1 + h), ±(1 − h2), 0)
- (±(1 − h2), 0, ±(1 + h))
其中h為過程中所產生之楔體的高,而五角十二面體的楔體高通常介於0到1之間。若高為1,則該形狀會變為菱形十二面體[7],若高為0,則五邊形會有一條邊共線成矩形、矩形會兩兩共面成正方形,而整體立體外觀為立方體。若其高為黃金分割率的乘法反元素−1 + √5/2[9],則會形成正十二面體;若是其相反數−1 − √5/2,則會形成大星形十二面體。
晶體學
[編輯]五角十二面體黃鐵礦中常見的晶體形狀[10],因此五角十二面體的英文名稱是由黃鐵礦的英文名稱來命名的[5]。雖然晶體學中並不存在正十二面體[11],但是與之拓樸同構的五角十二面體可以出現在黃鐵礦的晶體中,而且有可能是早期發現柏拉圖立體的來源之一[12]。而真正的正十二面體只能以準晶體的形式出現於部分準晶體之中,如鈥-鎂-鋅準晶體中。[13]
 立方體形的黃鐵礦晶體 |
 五角十二面體形的黃鐵礦晶體 |
相關多面體
[編輯]五角十二面體具有一種幾何自由度,該幾何自由度是在對應五角十二面體之面兩兩共面形成的立方體、和其中六條邊被縮短為0而退化形成的菱形十二面體的兩限制情況下的幾何自由度。而正十二面體則是所有邊等長的特殊中間體。[14]
| 1 : 1 | 0 : 1 | 1 : 1 | 2 : 1 | 1 : 1 | 0 : 1 | 1 : 1 |
|---|---|---|---|---|---|---|
| h = −√5 + 1/2 | h = -1 | h = -√5 + 1/2 | h = 0 | h = √5 − 1/2 | h = 1 | h = √5 + 1/2 |
 大星形十二面體是一種由正五角星組成的星形正多面體。 |
 退化。有12個頂點位於其幾何中心。 |
 凹等邊十二面體,又稱為內十二面體。 |
 將立方體的每個面分割成2個矩形的結構。 |
 在這一系列中既等邊又是凸的情況為正十二面體。 |
 6條邊退化成邊長0的情況為菱形十二面體 |
 邊自相交的等邊十二面體 |
二複合五角十二面體
[編輯]透過交和五角十二面體的非零座標可以形成另一個五角十二面體。這個新形成的五角十二面體可以和原本的五角十二面體組成一個具有對稱性的複合幾何結構,稱為二複合五角十二面體。其在考克斯特記號中可以用![]()
![]()
![]()
![]()
![]() 表示。這個複合立體具有八面體群對稱性。[15]
表示。這個複合立體具有八面體群對稱性。[15]
作為立方體分割面的變形結果
[編輯]五角十二面體可以透過將立方體6個面的每個面分割成2個矩形,並且相鄰面方向互相垂直的結構變形而來[7],而將立方體面分割成不同數量的矩形可以形成不同的結果,例如每個面皆分割成3個矩形可以形成立方五角十二面體,其對應的球面鑲嵌[註 1]是排球的常見形狀之一[16]。
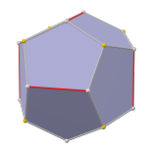
| 分割數 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 圖像 | 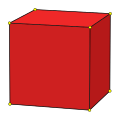
|
|

|

|
| 球面鑲嵌 | 
|

|

|

|
| 幾何結構 | 立方體 | 五角十二面體 | 立方五角十二面體 | 一種球面鑲嵌[17] |
參見
[編輯]註釋
[編輯]- ^ 一個多面體的球面鑲嵌或球面多面體是指將該多面體投影到球面上所形成的幾何結構。
參考文獻
[編輯]- ^ 五角十二面體 pyritohedron. 國家教育研究院. [2019-09-14]. (原始內容存檔於2021-08-14).
- ^ Crystal Habit (頁面存檔備份,存於互聯網檔案館). Galleries.com. Retrieved on 2016-12-02.
- ^ 中村慶三郎. 朝鮮コバルト鑛床調査概報. 地學雑誌 (公益社団法人 東京地學協會). 1942, 54 (6): 211––230.
- ^ 天然氣水合物能替代石油嗎?. 科學人雜誌 - 遠流. [2019-11-04]. (原始內容存檔於2021-08-16).
天然氣水合物常見的兩種籠狀結構為五角十二面體
- ^ 5.0 5.1 Pyrite. stonetrust. [2019-11-04]. (原始內容存檔於2019-02-23).
- ^ 超級立體家族-正多面體. ntsec.gov.tw. [2019-11-04]. (原始內容存檔於2009-04-14).
這三個條件都必須同時滿足,否則就不是正多面體,比如五角十二面體
- ^ 7.0 7.1 7.2 Koca, Nazife O and Al-Mukhaini, Aida Y and Koca, Mehmet and Al-Qanobi, Amal J. Symmetry of the pyritohedron and lattices. Sultan Qaboos University Journal for Science [SQUJS]. 2016, 21 (2): 139––149.
- ^ Koca, Nazife Ozdes and Koca, Mehmet and Al-Mukhaini, Aida and Al-Qanobi, Amal. Quaternionic Representations of the pyritohedral group, related polyhedra and lattices. arXiv preprint arXiv:1506.04600. 2015.
- ^ Weisstein, Eric W. (編). Golden Ratio Conjugate. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英語).
- ^ Cotton, F. A. Chemical Applications of Group Theory 3rd ed. New York: Wiley. 1990: p. 63.
- ^ George W. Hart. Dodecahedra. georgehart.com. 1996 [2019-11-04]. (原始內容存檔於2019-04-07).
- ^ Stephan. Klaus, Bianca. Violet, Katzengold: Pyrite, Plato, and a Polynomial (PDF), imaginary.org, 2015 [2019-11-04], (原始內容存檔 (PDF)於2016-07-05)
- ^ Mitch Jacoby. QUASICRYSTALS: A NEW KIND OF ORDER. SCIENCE/TECHNOLOGY, CENEAR. 1999-03-15, 77 (11): pp.44-47.
- ^ 藝術中的數學. shann.idv.tw. [2019-11-04]. (原始內容存檔於2021-08-14).
它是一種只具有正四面體對稱性的五角十二面體的特殊形式
- ^ George W. Hart. Compounds of Polyhedra. georgehart.com. 1996 [2019-11-04]. (原始內容存檔於2019-04-17).
- ^ Paul Bourke, § Volley ball (Gaelic football, Water polo, Netball), Geometry of sports balls, Paul Bourke, January 2017 [2019-11-04], (原始內容存檔於2018-07-27)
- ^ Hyde, Stephen T. Contemporary Geometry For The Built Design?. Architectural Theory Review (Taylor & Francis). 2010, 15 (2): 110––124.



