鏡像法 (又稱鏡像電荷法 )是一種解析靜電學 問題的基本工具。對於靜電學問題,鏡像法將原本問題的某些元素改換為假想電荷 ,同時保證仍然滿足定解問題原有的的邊界條件 (請參閱狄利克雷邊界條件 或諾伊曼邊界條件 )。
例如,給定一個由一片無限平面導體 和一個點電荷 構成的物理系統,這無限平面導體可以被視為一片鏡子,在鏡子裡面的鏡像電荷 與鏡子外面的點電荷,所形成的新系統,可以使得導體平面上的電場垂直於導體,與原本系統等價。藉此方法,我們可以將問題簡化,很容易地計算出導體外的電勢 、導體的表面感應電荷密度 、總感應電荷 等等。
鏡像法的有效性是唯一性定理 的必然結果,該定理指出如果指定了在體積 V 的整個區域內的電荷密度和 V 的所有邊界上的電位值,區域 V 內的電位唯一確定。另外,應用此結果到高斯定理的微分形式就能表明,在由導體包圍的包含電荷密度為 ρ 的體積 V 中,如果每個導體所帶電荷已經給出,那麼電場是唯一確定的。擁有電勢或電場的信息以及相應邊界條件,只要在指定區域的電荷分布滿足泊松方程並設定正確的邊界值,我們就可以把我們考慮的電荷分布換為更容易分析的結構。
[ 1]
唯一定理 表明,任意能夠滿足給定條件的解答,是唯一存在的解答。因此,給定條件唯一地決定了這解答。
舉例而言,假若,在一個三維空間區域裏,電勢
ϕ
{\displaystyle \phi }
∇
2
ϕ
=
f
{\displaystyle \nabla ^{2}\phi =f}
而在區域的表面,又滿足邊界條件
ϕ
=
g
{\displaystyle \phi =g}
其中,
f
{\displaystyle f}
g
{\displaystyle g}
函數 ,
則
ϕ
(
x
,
y
,
z
)
{\displaystyle \phi (x,\,y,\,z)}
唯一性定理適用於以下三種邊界情況:
給出了整個邊界的勢函數;
給出整個邊界的勢函數的法嚮導函數;
給出整個邊界部分場的勢函數和其他部分的勢函數的法嚮導函數; 應用唯一定理於鏡像法,只要問題能夠給足上述任意一種邊界條件,則求得的電勢函數解答必定是唯一的正確解答。
原本系統。位於 xy-平面的是一個接地 的無限平面導體。其上方的點電荷
q
{\displaystyle q}
(
0
,
0
,
a
)
{\displaystyle (0,\,0,\,a)}
鏡像法的新系統。坐標是
(
0
,
0
,
−
a
)
{\displaystyle (0,\,0,\,-a)}
−
q
{\displaystyle -q}
舉一個簡單的例子,如右圖所示,設定一個接地 的無限平面導體於 xy-平面,其上方有一個點電荷
q
{\displaystyle q}
(
0
,
0
,
a
)
{\displaystyle (0,\,0,\,a)}
庫侖定律 和相關靜電理論,這物理系統的各種物理量 ,像導體表面的電荷分佈,或點電荷所感受到的作用力,都不是很容易可以計算求得。
應用鏡像法,可以將無限平面導體改換成一個鏡像電荷,坐標是
(
0
,
0
,
−
a
)
{\displaystyle (0,\,0,\,-a)}
−
q
{\displaystyle -q}
(
x
,
y
,
z
)
,
z
>
0
{\displaystyle (x,\,y,\,z),\ z>0}
在新系統裏,應用庫侖定律,可以很容易地計算出點電荷所感受到的作用力。
採用圓柱坐標
(
ρ
,
ϕ
,
z
)
{\displaystyle (\rho ,\,\phi ,\,z)}
V
(
ρ
,
z
)
{\displaystyle V(\rho ,\,z)}
方位角
ϕ
{\displaystyle \phi }
V
(
ρ
,
z
)
=
1
4
π
ϵ
0
(
q
ρ
2
+
(
z
−
a
)
2
+
−
q
ρ
2
+
(
z
+
a
)
2
)
{\displaystyle V(\rho ,\,z)={\frac {1}{4\pi \epsilon _{0}}}\left({\frac {q}{\sqrt {\rho ^{2}+(z-a)^{2}}}}+{\frac {-q}{\sqrt {\rho ^{2}+(z+a)^{2}}}}\right)}
根據唯一定理 ,這解答是原本問題的唯一解答。
無限平面導體的表面電荷密度
σ
(
ρ
)
{\displaystyle \sigma (\rho )}
σ
=
−
ϵ
0
∂
V
∂
z
|
z
=
0
=
−
q
a
2
π
(
ρ
2
+
a
2
)
3
/
2
{\displaystyle \sigma =-\epsilon _{0}{\frac {\partial V}{\partial z}}{\Bigg |}_{z=0}=-\ {\frac {qa}{2\pi (\rho ^{2}+a^{2})^{3/2}}}}
積分表面電荷密度於無限平面導體,可以得到無限平面導體的總感應電量
Q
t
{\displaystyle Q_{t}}
Q
t
{\displaystyle Q_{t}}
=
∫
0
2
π
∫
0
∞
σ
(
ρ
)
ρ
d
ρ
d
θ
{\displaystyle =\int _{0}^{2\pi }\int _{0}^{\infty }\sigma \left(\rho \right)\,\rho \,d\rho \,d\theta }
=
−
q
a
2
π
∫
0
2
π
d
θ
∫
0
∞
ρ
d
ρ
(
ρ
2
+
a
2
)
3
/
2
{\displaystyle =-\ {\frac {qa}{2\pi }}\int _{0}^{2\pi }d\theta \int _{0}^{\infty }{\frac {\rho \,d\rho }{\left(\rho ^{2}+a^{2}\right)^{3/2}}}}
=
−
q
{\displaystyle =-q}
答案非常簡單,就是
−
q
{\displaystyle -q}
這問題指引出一個更進階的問題:給予一對平行的無限平面導體,其中間有一個點電荷,求兩片無限平面導體之間的電勢?這是一個非常有意思,值得研習的問題[ 2]
所有二面角成
α
=
2
π
n
{\displaystyle \alpha ={\frac {2\pi }{n}}}
n
{\displaystyle n}
n
−
1
{\displaystyle n-1}
[來源請求]
延伸至兩個點電荷的物理系統。 鏡像法可以延伸至兩個或多於兩個點電荷。只要對於每一個點電荷,都添加一個對應的鏡像電荷。根據疊加原理 ,總電勢等於所有點電荷、鏡像電荷產生的電勢的總和。在 xy-平面的任意一位置,點電荷產生的電勢會與其鏡像電荷產生的電勢相抵消。因此,在 xy-平面的任意一位置,總電勢等於零,滿足邊界條件。
圖右展示一個物理系統案例,裡面有兩個真實的點電荷和一個無限平面導體,兩個點電荷的坐標分別是
(
x
1
,
y
1
,
z
1
)
{\displaystyle (x_{1},\,y_{1},\,z_{1})}
(
x
2
,
y
2
,
z
2
)
{\displaystyle (x_{2},\,y_{2},\,z_{2})}
q
1
{\displaystyle q_{1}}
q
2
{\displaystyle q_{2}}
(
x
1
,
y
1
,
−
z
1
)
{\displaystyle (x_{1},\,y_{1},\,-z_{1})}
(
x
2
,
y
2
,
−
z
2
)
{\displaystyle (x_{2},\,y_{2},\,-z_{2})}
−
q
1
{\displaystyle -q_{1}}
−
q
2
{\displaystyle -q_{2}}
假設,在無限平面導體上方,有一個電偶極子 ,其電偶極矩 是
M
=
(
M
x
,
M
y
,
M
z
)
{\displaystyle \mathbf {M} =(M_{x},\,M_{y},\,M_{z})}
(
x
,
y
,
z
)
{\displaystyle (x,\,y,\,z)}
M
′
=
(
M
x
,
M
y
,
−
M
z
)
{\displaystyle \mathbf {M} '=(M_{x},\,M_{y},\,-M_{z})}
(
x
,
y
,
−
z
)
{\displaystyle (x,\,y,\,-z)}
應用鏡像法於半徑為
R
{\displaystyle R}
球坐標系 的原點於圓球殼殼心。綠點是點電荷
q
{\displaystyle q}
P
{\displaystyle \mathbf {P} }
−
q
R
/
p
{\displaystyle -qR/p}
R
2
/
p
{\displaystyle R^{2}/p}
r
=
R
{\displaystyle r=R}
鏡像法也可以應用於圓球殼導體[ 3]
如圖右,採用原點位於圓球殼殼心的球坐標系 。被置於真空中的接地 的圓球殼,其半徑為
R
{\displaystyle R}
q
{\displaystyle q}
P
{\displaystyle \mathbf {P} }
−
q
R
/
p
{\displaystyle -qR/p}
R
2
/
p
{\displaystyle R^{2}/p}
r
{\displaystyle \mathbf {r} }
疊加 為
4
π
ϵ
0
V
(
r
)
=
q
|
r
1
|
+
(
−
q
R
/
p
)
|
r
2
|
=
q
r
2
+
p
2
−
2
r
⋅
p
+
(
−
q
R
/
p
)
r
2
+
R
4
p
2
−
2
R
2
p
2
r
⋅
p
{\displaystyle 4\pi \epsilon _{0}V(\mathbf {r} )={\frac {q}{|\mathbf {r} _{1}|}}+{\frac {(-qR/p)}{|\mathbf {r} _{2}|}}={\frac {q}{\sqrt {r^{2}+p^{2}-2\mathbf {r} \cdot \mathbf {p} }}}+{\frac {(-qR/p)}{\sqrt {r^{2}+{\frac {R^{4}}{p^{2}}}-{\frac {2R^{2}}{p^{2}}}\mathbf {r} \cdot \mathbf {p} }}}}
經過一番運算,可以得到
V
(
r
)
=
1
4
π
ϵ
0
[
q
r
2
+
p
2
−
2
r
⋅
p
−
q
r
2
p
2
R
2
+
R
2
−
2
r
⋅
p
]
{\displaystyle V(\mathbf {r} )={\frac {1}{4\pi \epsilon _{0}}}\left[{\frac {q}{\sqrt {r^{2}+p^{2}-2\mathbf {r} \cdot \mathbf {p} }}}-{\frac {q}{\sqrt {{\frac {r^{2}p^{2}}{R^{2}}}+R^{2}-2\mathbf {r} \cdot \mathbf {p} }}}\right]}
請注意,在圓球殼(
r
=
R
{\displaystyle r=R}
r
<
R
{\displaystyle r<R}
V
(
r
)
{\displaystyle V(\mathbf {r} )}
r
>
R
{\displaystyle r>R}
V
(
r
)
{\displaystyle V(\mathbf {r} )}
σ
{\displaystyle \sigma }
天頂角
θ
{\displaystyle \theta }
σ
(
θ
)
=
ϵ
0
∂
V
∂
r
|
r
=
R
=
−
q
(
R
2
−
p
2
)
4
π
R
(
R
2
+
p
2
−
2
p
R
cos
θ
)
3
/
2
{\displaystyle \sigma (\theta )=\epsilon _{0}{\frac {\partial V}{\partial r}}{\Bigg |}_{r=R}={\frac {-q(R^{2}-p^{2})}{4\pi R(R^{2}+p^{2}-2pR\cos \theta )^{3/2}}}}
積分感應電荷密度於所有立體角 ,則可以得到在圓球殼的總感應電量
Q
t
{\displaystyle Q_{t}}
Q
t
=
∫
0
π
d
θ
∫
0
2
π
d
ϕ
σ
(
θ
)
R
2
sin
θ
=
−
q
{\displaystyle Q_{t}=\int _{0}^{\pi }d\theta \int _{0}^{2\pi }d\phi \,\,\sigma (\theta )R^{2}\sin \theta =-q}
由於總感應電量與點電荷電量的代數和 等於零,所以整個物理系統的總電量等於零。圓球殼導體能夠除去點電荷所造成的非球形對稱性 。在圓球殼以外的物理是球形對稱的。應用高斯定律 ,可以計算出電場
E
{\displaystyle \mathbf {E} }
E
=
0
{\displaystyle \mathbf {E} =\mathbf {0} }
假設圓球殼不接地,則圓球殼外表面的感應電荷密度是
σ
=
q
/
4
π
R
2
{\displaystyle \sigma =q/4\pi R^{2}}
圓球殼外,離圓心距離為
r
{\displaystyle r}
E
{\displaystyle \mathbf {E} }
E
=
q
4
π
ϵ
0
r
2
r
^
{\displaystyle \mathbf {E} ={\frac {q}{4\pi \epsilon _{0}r^{2}}}{\hat {\mathbf {r} }}}
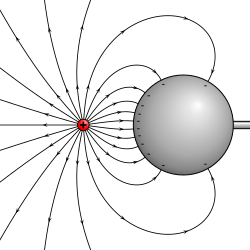
接地圓球導體殼外的電場線。 請注意,這問題的逆反問題也可以用鏡像法解析。在一個半徑為
R
{\displaystyle R}
q
{\displaystyle q}
p
{\displaystyle \mathbf {p} }
p
{\displaystyle p}
−
q
R
/
p
{\displaystyle -qR/p}
(
R
2
/
p
2
)
p
{\displaystyle (R^{2}/p^{2})\mathbf {p} }
鏡像法對於電偶極矩 的計算公式比較複雜。假若我們將電偶極子 視為一對距離很近的點電荷,則鏡像電偶極子 的電量和電偶極矩都會有所改變。給予電偶極子的電偶極矩為
M
{\displaystyle \mathbf {M} }
p
{\displaystyle \mathbf {p} }
R
{\displaystyle R}
(
R
2
/
p
2
)
p
{\displaystyle (R^{2}/p^{2})\mathbf {p} }
q
′
=
R
p
⋅
M
p
3
{\displaystyle q'={\frac {R\mathbf {p} \cdot \mathbf {M} }{p^{3}}}}
電偶極矩為
M
′
=
R
3
[
−
M
p
3
+
2
p
(
p
⋅
M
)
p
5
]
{\displaystyle \mathbf {M} '=R^{3}\left[-{\frac {\mathbf {M} }{p^{3}}}+{\frac {2\mathbf {p} (\mathbf {p} \cdot \mathbf {M} )}{p^{5}}}\right]}
鏡像法的圓球殼計算方式直接地引導出反演法 。採用球坐標
(
r
,
θ
,
ϕ
)
{\displaystyle (r,\,\theta ,\,\phi )}
調和函數
Φ
(
r
,
θ
,
ϕ
)
{\displaystyle \Phi (r,\,\theta ,\,\phi )}
R
{\displaystyle R}
Φ
′
(
r
,
θ
,
ϕ
)
=
R
r
Φ
(
R
2
r
,
θ
,
ϕ
)
{\displaystyle \Phi '(r,\,\theta ,\,\phi )={\frac {R}{r}}\Phi \left({\frac {R^{2}}{r}},\,\theta ,\,\phi \right)}
給予一集合的點電荷,位置和電量分別為
(
r
i
,
θ
i
,
ϕ
i
)
{\displaystyle (r_{i},\,\theta _{i},\,\phi _{i})}
q
i
{\displaystyle q_{i}}
Φ
{\displaystyle \Phi }
Φ
′
{\displaystyle \Phi '}
(
R
2
/
r
i
,
θ
i
,
ϕ
i
)
{\displaystyle (R^{2}/r_{i},\,\theta _{i},\,\phi _{i})}
R
q
i
/
r
i
{\displaystyle Rq_{i}/r_{i}}
ρ
(
r
,
θ
,
ϕ
)
{\displaystyle \rho (r,\,\theta ,\,\phi )}
Φ
{\displaystyle \Phi }
Φ
′
{\displaystyle \Phi '}
ρ
′
(
r
,
θ
,
ϕ
)
=
(
R
/
r
)
5
ρ
(
R
2
/
r
,
θ
,
ϕ
)
{\displaystyle \rho '(r,\,\theta ,\,\phi )=(R/r)^{5}\rho (R^{2}/r,\,\theta ,\,\phi )}
帕松方程式的唯一定理 (Uniqueness theorem for Poisson's equation )恩紹定理 (Earnshaw's theorem )互易定理 (Reciprocity (electromagnetism))多極展開
^
David J. Griffiths. Introduction to Electrodynamics (4th Ed.). Glenview, IL: Pearson. 2013: 121. ISBN 0-321-85656-2
^ Dick, B. G., Images and the Point Charge-Capacitor Problem, American Journal of Physics, 1973, 41 (11): pp. 1289–1290 ^ Tikhonov, A. N.; Samarskii, A. A. Equations of Mathematical Physics. New York: Dover Publications. 1963. ISBN 0-486-66422-8















































![{\displaystyle V(\mathbf {r} )={\frac {1}{4\pi \epsilon _{0}}}\left[{\frac {q}{\sqrt {r^{2}+p^{2}-2\mathbf {r} \cdot \mathbf {p} }}}-{\frac {q}{\sqrt {{\frac {r^{2}p^{2}}{R^{2}}}+R^{2}-2\mathbf {r} \cdot \mathbf {p} }}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52743d0a81a388b2953818dd92243520c7b21231)

















![{\displaystyle \mathbf {M} '=R^{3}\left[-{\frac {\mathbf {M} }{p^{3}}}+{\frac {2\mathbf {p} (\mathbf {p} \cdot \mathbf {M} )}{p^{5}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3546c8e9d0d782e6a1f35dfbaf85e9cc0798b03)











