跳至內容

六角四片四角孔扭歪無限面體

編輯連結
本頁使用了標題或全文手工轉換
維基百科，自由的百科全書
六角四片四角孔扭歪無限面體
六角四片四角孔扭歪無限面體
（點選檢視旋轉模型）
類別正扭歪無限面體
對偶多面體四角六片四角孔扭歪無限面體
識別
鮑爾斯縮寫
（verse-and-dimensions的wikia：Bowers acronym）		muo在維基數據編輯
數學表示法
考克斯特符號
（英語：Coxeter-Dynkin diagram）		branch_11 4a4b nodes 
施萊夫利符號{6,4|4}
性質
面無限個正六邊形
邊無限
頂點無限
4個正六邊形的公共頂點
組成與佈局
頂點圖扭歪四邊形
{4}#{ }
頂點佈局
（英語：Vertex_configuration）		同於截角八面體堆砌
特性
扭歪、點可遞
圖像
立體圖
扭歪四邊形
{4}#{ }
（頂點圖）

四角六片四角孔扭歪無限面體
（對偶多面體）

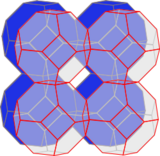
在幾何學中，六角四片四角孔扭歪無限面體 （英語：muoctahedron、日語：六角四片四角孔ねじれ正多面体[1]）是一種正扭歪無限面體，是一個由六邊形組成且發散的多面體，其多面體所形成的結構無法包覆一個三維空間區域，因此屬於扭歪多面體，其可以視為從截角八面體堆砌（截角八面體的空間填充的形狀）中移除所有正方形之後所形成的幾何結構。

性質

[編輯]

六角四片四角孔扭歪無限面體由無限多個正六邊形組成[2]，具有無線條邊和無限多個頂點，每個頂點都是4個正六邊形的公共頂點，並具有正方形的孔洞，在施萊夫利符號中可以用{6,4|4}來表示，在頂點圖中，亦能使用6.6.6.6來表示[3]，其對偶多面體為四角六片四角孔扭歪無限面體[4]。

二面角

[編輯]

六角四片四角孔扭歪無限面體由無限多個正六邊形組成，每個正六邊形與正六邊形的夾角以扭歪的形式交錯以截角八面體的六邊形-六邊形二面角與其反角組成，其角度等於截角八面體的六邊形-六邊形二面角[5]：

由於其角為正角與反角交錯，因而使其所形成的幾何結構發散，並形成了具有特定孔洞的幾何結構，此種幾何結構最早由考克斯特描述[6][7]。

六角四片四角孔扭歪無限面體頂角與二面角的構成模式
六角四片四角孔扭歪無限面體頂角示意圖，藍色為其構成面。

頂角的組成

[編輯]

六角四片四角孔扭歪無限面體每個頂角都是由四個六邊形構成的四面角，由於其二面角的交錯結構，因此其頂點圖是一個扭歪四邊形，換句話說即其頂角沿線切開後的形狀不是一個凸多邊形

用途

[編輯]

六角四片四角孔扭歪無限面體通常用於裝置藝術，例如茶几、貓的藏身處、透過其孔洞製造氣氛照明裝置或做成可堆疊雕塑[2]。

相關多面體

[編輯]

對偶複合體

[編輯]
複合四角六片四角孔扭歪無限面體六角四片四角孔扭歪無限面體
六角四片四角孔扭歪無限面體
複合四角六片四角孔扭歪無限面體六角四片四角孔扭歪無限面體
類別複合正扭歪無限多面體
對偶多面體自身對偶
性質
體2
面無限個正六邊形
無限個正方形
邊無限
頂點無限
4個正六邊形的公共頂點
6個正方形的公共頂點
組成與佈局
複合幾何體數量2
複合幾何體種類1個四角六片四角孔扭歪無限面體
1個六角四片四角孔扭歪無限面體

對偶複合體，即一個多面體與其對偶多面體組合成的複合圖形。六角四片四角孔扭歪無限面體為複合四角六片四角孔扭歪無限面體六角四片四角孔扭歪無限面體，在施萊夫利符號中用{4,6|4}{6,4|4}表示。

相關堆砌體

[編輯]
主條目：截角八面體堆砌

六角四片四角孔扭歪無限面體可以看做是由截角八面體的空間填充的形狀——截角八面體堆砌中移除所有正方形面、只保留正六邊形面的後所形成的扭歪無限面體[8]，因此，六角四片四角孔扭歪無限面體與截角八面體堆砌有著相同的頂點布局。

六角四片四角孔扭歪無限面體
六角四片四角孔扭歪無限面體 		骨架圖
截角八面體堆砌與
六角四片四角孔扭歪無限面體
的骨架圖相同 		截角八面體堆砌
截角八面體堆砌

正扭歪無限面體

[編輯]

六角四片四角孔扭歪無限面體是三種正扭歪無限面體之一，另外兩種為[10]：

圖像
四角六片四角孔扭歪無限面體
六角四片四角孔扭歪無限面體
六角六片三角孔扭歪無限面體
施萊夫利符號 {4,6|4} {6,4|4} {6,6|3}

商空間

[編輯]

六角四片四角孔扭歪無限面體在拓樸中相當於四階六邊形鑲嵌（施萊夫利符號：{6,4}）的商空間[11]，即六角四片四角孔扭歪無限面體可透過拓樸變形成四階六邊形鑲嵌。

其他六角扭歪無限面體

[編輯]

有些扭歪無限面體也是由六邊形組成的，例如六角六片三角孔扭歪無限面體。

參見

[編輯]


參考文獻

[編輯]
  1. ^ 1.0 1.1 正多面体を解く. Tokai library. 東海大學出版會. 2002 [2018-09-02]. ISBN 9784486015871. （原始內容存檔於2018-09-02）. 
  2. ^ 2.0 2.1 Apeirohedron stool. voukenaspetrides.com. [2019-05-04]. （原始內容存檔於2020-02-10）. 
  3. ^ Yackel, C. and belcastro, sarah-marie. Figuring Fibers. Miscellaneous Books. American Mathematical Society. 2018 [2019-05-04]. ISBN 9781470429317. （原始內容存檔於2019-11-29）. 
  4. ^ kotetu. 準結晶とウイルスの意外な関係. eonet.ne.jp. 2017-03-31 [2018-09-02]. （原始內容存檔於2017-08-13）. 
  5. ^ Archimedean Solids: TruncatedOctahedron. dmccooey.com. [2019-05-05]. （原始內容存檔於2019-10-31）. 
  6. ^ Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8
  7. ^ Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues, Proceedings of the London Mathematics Society, Ser. 2, Vol 43, 1937.)
  8. ^ 正多面體を解く2002 [1] 第6章　ねじれ正多面體：ねじれ多面體の具體的構成法
  9. ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5,
  10. ^ The Symmetry of Things, 2008[9], Chapter 23 Objects with Primary Symmetry, Infinite Platonic Polyhedra, pp. 333–335
  11. ^ Lee, Dami. Geometric realizations of cyclically branched coverings over punctured spheres (PDF). arXiv preprint arXiv:1809.06321. 2018 [2019-05-05]. （原始內容存檔 (PDF)於2019-05-05）. 
取自「https://wiki.c-s.workers.dev/w/index.php?title=六角四片四角孔扭歪無限面體&oldid=75192129」