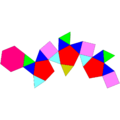
三角广底球状丸塔

三角广底球状罩帐

类别	詹森多面体 J91 - J92 - J1
识别
名称	三角广底球状罩帐
参考索引	J92
鲍尔斯缩写	thawro
性质
面	20
边	36
顶点	18
欧拉特征数	F=20, E=36, V=18 （χ=2）
组成与布局
面的种类	13个三角形 3个正方形 3个五边形 1个六边形
顶点图	3个(33.5) 6个(3.4.3.5) 3个(3.5.3.5) 2×3个(32.4.6)
对称性
对称群	C3v群
特性
凸
图像
（展开图）

三角广底球状罩帐（Triangular hebesphenorotunda）是约翰逊多面体的其中一个，索引为J₉₂。它无法由柏拉图立体（正多面体）和阿基米得立体（半正多面体）经过切割、增补而得来，是詹森多面体中的基本立体之一。詹森多面体是凸多面体，面皆由正多边形组成但不属于均匀多面体，共有92种。这些立体最早在1966年由诺曼·詹森（Norman Johnson）命名并给予描述。

虽然其无法由正多面体和半正多面体经过切割、增补而得来，但他其实与截半二十面体（半正多面体的一种）有著不可分离的关系，最明显的就是他们都有三个五边形和四个三角群位于立体的其中一边。如果将这些面与面一个个地被排列在截半二十面体上，那么唯一的六边形面就会位于平面上两相对的三角形面中间。

三角广底球状罩帐还存在可以与小斜方截半二十面体相应面对齐的部分，即3个新月状的三角形-正方形-三角形带。其位于顶点图表示为(3³.5)的顶点周围也可以与正二十面体欠侧锥的相应面对齐。

诺曼·詹森使用前缀hebespheno-（广底球状）来指代由三个相邻的新月状（lunes）形成的钝楔状复合结构，新月状（lunes）是一个正方形和两个正三角形连接在正方形相对两侧的结构。 后缀（triangular）-rotunda（罩帐）是指三个正三角形和三个正五边形围绕另一个正三角形的复合结构，其结构类似于五角罩帐。

性质

三角广底球状罩帐共由20个面、36条边和18个顶点组成。在其20个面中，有13个正三角形、3个正方形、3个五边形和1个六边形。在其18个顶点中，有3个顶点是2个三角形和2个五边形的公共顶点，并且这些面在构成顶角的多面角时，以三角形、五边形、三角形和五边形的顺序排列，在顶点图中可以用(3.5.3.5)来表示，或者简写为[(3,5)²]；还有6个顶点是2个三角形、1个正方形和1个五边形的公共顶点，并且这些面在构成顶角的多面角时，以三角形、正方形、三角形和五边形的顺序排列，在顶点图中可以用(3.4.3.5)或[3,4,3,5]来表示；还有3个顶点是3个三角形和1个五边形的公共顶点，在顶点图中可以用(3³.5)或[3³,5]来表示；剩下的6个顶点是2个三角形、1个正方形和1个六边形的公共顶点，并且这些面在构成顶角的多面角时，以三角形、三角形、正方形和六边形的顺序排列，在顶点图中可以用(3².4.6)或[3²,4,6]来表示。

结构

三角广底球状罩帐是诺曼·詹森列表末尾的特殊詹森多面体之一，它无法由柏拉图立体（正多面体）和阿基米得立体（半正多面体）经过切割、增补而得来。然而，它与截半二十面体密切相关。在其表面的顶部的3个五边形和3个三角形围绕著一个中心三角形的结构，实际上是截半二十面体表面的一部分。此外，其六边形面位于能够平分对应截半二十面体的平面上。

体积与表面积

若一个三角广底球状罩帐边长为$a$，则其表面积$A$为：

$A=\left(3+{\frac {1}{4}}{\sqrt {1308+90{\sqrt {5}}+114{\sqrt {75+30{\sqrt {5}}}}}}\right)a^{2}\approx 16.38867a^{2},$

而其体积$V$为：

$V={\frac {1}{6}}\left(15+7{\sqrt {5}}\right)a^{3}\approx 5.10875a^{3}.$

二面角

三角广底球状罩帐共有7种二面角，分别是两种三角形与正方形的二面角、两种三角形与五边形的二面角、一种三角形与三角形的二面角、一种三角形与六边形的二面角以及一种正方形与六边形的二面角。

其中，两种三角形与正方形的二面角分为在“新月”部分上的，以及“新月”与“罩帐”交错部分的。

其中，“新月”部分上的三角形与正方形的二面角角度约为159.09度：

$\arccos \left(-{\frac {1+{\sqrt {5}}}{\sqrt {12}}}\right)\approx 2.7767288\approx 159.094843^{\circ }$

而“新月”与“罩帐”交错部分的三角形与正方形的二面角角度约为110.9度：

$\arccos \left(-{\sqrt {\frac {3-{\sqrt {5}}}{6}}}\right)\approx 1.935660\approx 110.905157^{\circ }$

两种三角形与五边形的二面角分为在“罩帐”部分上的，以及“新月”与“罩帐”交错部分的。

其中，“罩帐”部分上的三角形与五边形的二面角角度约为142.62度：

$\arccos \left(-{\sqrt {\frac {5+2{\sqrt {5}}}{15}}}\right)\approx 2.48923451\approx 142.622632^{\circ }$

而“新月”与“罩帐”交错部分的三角形与五边形的二面角角度约为100.81度：

$\arccos \left(-{\sqrt {\frac {5-2{\sqrt {5}}}{15}}}\right)\approx 1.75950686\approx 100.812317^{\circ }$

三角形与三角形的二面角以及三角形与六边形的二面角皆为负五平方根三分之一的反馀弦值，角度约为138.19度：

$\angle$三角形$,$三角形$\,=\angle$三角形$,$六边形$\,=\arccos \left(-{\frac {\sqrt {5}}{3}}\right)\approx 2.411864997\approx 138.189685^{\circ }$

正方形与六边形的二面角角度约为110.9度：

$\angle$正方形$,$六边形$\,=\arccos \left(-{\sqrt {\frac {3-{\sqrt {5}}}{6}}}\right)\approx 1.935660\approx 110.905157^{\circ }$

顶点座标

边长为${\sqrt {5}}-1$的三角广底球状罩帐的顶点座标由下列顶点的轨道的并集在绕z轴旋转120°和沿yz平面镜射所产生的空间对称群之群作用下给出：

$\left(0,-{\frac {2}{\tau {\sqrt {3}}}},{\frac {2\tau }{\sqrt {3}}}\right),\left(\tau ,{\frac {1}{{\sqrt {3}}\tau ^{2}}},{\frac {2}{\sqrt {3}}}\right),$

$\left(\tau ,-{\frac {\tau }{\sqrt {3}}},{\frac {2}{{\sqrt {3}}\tau }}\right),\left({\frac {2}{\tau }},0,0\right),$

此处的$\tau ={\frac {{\sqrt {5}}+1}{2}}$（有时写作$\varphi$）为黄金比例。第一个点生成与六边形面相对的三角形面，第二个点生成围绕前一个三角形面的底，第三个点生成与第一个三角形相对的五边形尖端，最后一个点生成六边形。

参见

• 约翰逊多面体
• 截半二十面体
• 正多面体

外部链接

• 埃里克·韦斯坦因. Johnson solids. MathWorld. 
  • 埃里克·韦斯坦因. Triangular hebesphenorotunda. MathWorld.