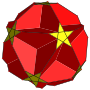
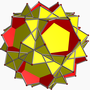
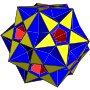
反扭稜小星形十二面體
 | ||||
| 類別 | 均勻星形多面體 | |||
|---|---|---|---|---|
| 對偶多面體 | 中逆五角六十面体 | |||
| 識別 | ||||
| 名稱 | 反扭稜小星形十二面體 Inverted snub dodecadodecahedron | |||
| 參考索引 | U60, C76, W114 | |||
| 鮑爾斯縮寫 | isdid | |||
| 數學表示法 | ||||
| 考克斯特符號 | ||||
| 施萊夫利符號 | sr{5⁄3,5} | |||
| 威佐夫符號 | | 5⁄3 2 5[3][4][5] | 2 5⁄3 5[6]:180[7] | |||
| 性質 | ||||
| 面 | 84 | |||
| 邊 | 150 | |||
| 頂點 | 60 | |||
| 歐拉特徵數 | F=84, E=150, V=60 (χ=-6) | |||
| 組成與佈局 | ||||
| 面的種類 | 20個正三角形 12個正五邊形 12個正五角星 | |||
| 頂點圖 | 3.3.5.3.5⁄3 | |||
| 對稱性 | ||||
| 對稱群 | Ih, [5,3]+, 532 | |||
| 圖像 | ||||
| ||||
在幾何學中,反扭稜小星形十二面體是一種星形均勻多面體,索引為U60[5],是中逆五角六十面体的對偶多面體[7],並且與扭稜小星形十二面體拓樸同構[8]。
性質
[编辑]反扭稜小星形十二面體共由84個面、150條邊和60個頂點組成[5],歐拉示性數為-6[3]。在其84個面中,有60個正三角形面、12個正五邊形面和12個正五角星面[9]其60個頂點每個頂點都是1個正十角星、1個五角星和3個三角形的公共頂點,並且這些面在頂都周圍皆是依照三角形、反向相接的五角星、三角形、三角形、五邊形和三角形的順序排列,在頂點圖中可以用(3,5⁄3,3,3,5)[5][10]、(5⁄3,3,3,5,3)[1][3]或(5.3.5⁄3.3.3)[11]來表示。
表示法
[编辑]反扭稜小星形十二面體在考克斯特—迪肯符号中可以表示為![]()
![]()
![]()
![]()
![]()
![]()
![]() [1][2],在施莱夫利符号中可以表示為sr{5⁄3,5},在威佐夫記號中可以表示為| 5⁄3 2 5
[3][4][5]或| 2 5⁄3 5[6]:180[7]。
[1][2],在施莱夫利符号中可以表示為sr{5⁄3,5},在威佐夫記號中可以表示為| 5⁄3 2 5
[3][4][5]或| 2 5⁄3 5[6]:180[7]。
二面角
[编辑]反扭稜小星形十二面體有三種二面角,分別為五邊形面和三角形面的二面角、三角形面和三角形面的二面角以及五角星面和三角形面的二面角。其中五邊形面和三角形面的二面角的值為多項式4100625 x8-32805000 x7+95863500 x6-119799000 x5+68311350 x4-20763000 x3+7189740 x2-2234280 x+201601之正實根(約為0.132650687)的平方根(約為0.36421242)的反餘弦值,約為68.640878254度[12];三角形面和三角形面的二面角的值為多項式6561 x4-20412 x3+30942 x2-20556 x+4489之正實根(約為0.4216231174)的負平方根的反餘弦值,約為130.490738467度[12];五角星面和三角形面的二面角的值為多項式4100625 x8-32805000 x7+95863500 x6-119799000 x5+68311350 x4-20763000 x3+7189740 x2-2234280 x+201601之正實根(約為0.9627736877)的平方根(約為0.9812103178)的反餘弦值,約為11.124480107度。[12]
尺寸
[编辑]若反扭稜小星形十二面體的邊常為單位長,則其外接球半徑為多項式之較小正實根(約為0.72527)的平方根[12],約為0.8516302[13]。
相關多面體
[编辑]兩個反扭稜小星形十二面體可以複合成均勻複合體,稱為二複合反扭稜小星形十二面體[14]。
 二複合反扭稜小星形十二面體 |
參見
[编辑]參考文獻
[编辑]- ^ 1.0 1.1 1.2 Klitzing, Richard. Axial-Symmetrical Edge-Facetings of Uniform Polyhedra (PDF). tic. 2002, 2 (4): 3 [2022-08-14]. (原始内容存档 (PDF)于2022-08-14).
- ^ 2.0 2.1 Richard Klitzing. Icosahedral Symmetries uniform polyhedra, Polytopes & their Incidence Matrices. bendwavy.org. [2022-08-07]. (原始内容存档于2018-07-07).
- ^ 3.0 3.1 3.2 3.3 Har'El, Zvi. Uniform solution for uniform polyhedra (PDF). Geometriae Dedicata (Springer). 1993, 47 (1): 57–110 [2022-08-14]. (原始内容存档 (PDF)于2018-06-19).
- ^ 4.0 4.1 V.Bulatov. inverted snub dodecadodecahedron. [2022-08-14]. (原始内容存档于2022-08-14).
- ^ 5.0 5.1 5.2 5.3 5.4 Roman E. Maeder. 60: inverted snub dodecadodecahedron. mathconsult.ch. [2022-08-14]. (原始内容存档于2022-05-25).
- ^ 6.0 6.1 Wenninger, M.J. Polyhedron Models. Cambridge University Press. 1974 [2021-09-05]. ISBN 9780521098595. LCCN 69010200. (原始内容存档于2021-08-31).
- ^ 7.0 7.1 7.2 Weisstein, Eric W. (编). Inverted Snub Dodecadodecahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Richard Klitzing. isdid, inverted snub dodecadodecahedron. bendwavy.org. [2022-08-14]. (原始内容存档于2022-08-17).
- ^ Jonathan Bowers. Polyhedron Category 6: Snubs. polytope.net. (原始内容存档于2021-10-19).
- ^ Zvi Har'El. Kaleido Data: Uniform Polyhedron #65, inverted snub dodecadodecahedron. harel.org.il. 2006-11-14 [2022-08-14]. (原始内容存档于2022-08-14).
- ^ Kovič, J. Classification of uniform polyhedraby their symmetry-type graphs (PDF). Int. J. Open Problems Compt. Math. 2012, 5 (4) [2022-08-14]. (原始内容存档 (PDF)于2022-08-14).
- ^ 12.0 12.1 12.2 12.3 David I. McCooey. Self-Intersecting Snub Quasi-Regular Polyhedra: Inverted Snub Dodecadodecahedron. [2022-08-14]. (原始内容存档于2022-08-14).
- ^ Eric W. Weisstein. Inverted Snub Dodecadodecahedron. archive.lib.msu.edu. 1999-05-26 [2022-08-14]. (原始内容存档于2013-06-21).
- ^ Skilling, John, Uniform Compounds of Uniform Polyhedra, Mathematical Proceedings of the Cambridge Philosophical Society, 1976, 79: 447–457, MR 0397554, doi:10.1017/S0305004100052440